गोष्ट सांगा गणित शिकवा... 7

तुमची सावली "गायब" होईल! (पुण्यात - 13 मे रोजी दु. 12:31 वा.) Fake news? खाली लिंक्स आणि सविस्तर माहिती दिली आहे. ************************** "ओ शी*" ... अचानक सगळे बंद पडल्यामुळे सायली आणि चिंट्या चांगलेच चिडले. क्वचितच वैतागणारा सॅमी देखील स्वतःला आवरू शकला नाही. डोळ्यावरचा 3D हेडसेट मधे फक्त काळोख दिसत होता... लाईट नाही गेले, मी ब्राउजर बंद केला... नेहाने हळूच सांगीतलं... रागीट नजरा आता नेहाकडे वळल्या. 3चा अलार्म वाजला, आपलं ठरलं आहे थांबायचं म्हणून... नेहाने सफाई दिली... चांगलेच भांडण झाले,... ************************** आत्ता पर्यंत: अंतराळात भ्रमण करून ज्ञानाच्या सीमा वाढवण्याच्या मोहिमेवर टीम पुणेला आय आर एस आर्यभट्टवर कॅप्टन नेमोंनी सहकारी म्हणून स्वीकारलं होतं. सध्या त्रिकोणी ग्रहावर... एरेटॉसथिनिस काका... गोष्टीचा आधीचा भाग.... इथे टिचकी मारा ************************** पण आता उपाय नव्हता. पुन्हा लॉग इन व्हायला नेहा तयार नव्हती... आणि तिच्या सहभागाशिवाय सिस्टिम चालेना! नाइलाजाने सगळे घराकडे चालू लागले... पण धुसफुस चालूच होती. रविवारी नेहा मीटिंग प्लेसला आली नव्हती... तेव्हा सायलीला राहवले नाही. घडल्या प्रकारचा राग बोलून दाखवला. चिंट्याने सुद्धा त्यात सूर मिसळला. पण सॅमी आता शांत होता. दोघांचा जोर थोडा ओसरला तसे त्यांनी समजावले. गोष्ट किती मोठी होती, इंटरेस्टिंग होती काहीच माहीत नव्हतं. चांगली असेल तर अर्ध्यात तोडण्यापेक्षा, ... पण असा काय प्रॉब्लेम झाला असता थोडं सेशन लांबला तर?... एखाद्यावेळी चालतं!... किती लांबलं तर चालेल?... त्यापेक्षा तयारीने पुढच्या वेळेला जाणे योग्य नाही का?... दोघांना तरीही पटेना. शेवटी सॅमी म्हणाला... ठीक आहे, आपण सांगू तसे तिला. पेनालटी म्हणून भेळ–पाणीपुरी पार्टी उकळायची ठरलं... शाळेतही त्रिकोणमितीचेच धडे चालले होते... सर सांगत होते... प्रत्यक्ष मोजण्यास अवघड अशी डोंगराची किंवा तत्सम गोष्टींची उंचीची अचूक मोजमाप त्रिकोणमितीच्या साहाय्याने सहजपणे करता येते. स्थापत्यशास्त्रात मोठाले प्रकल्प, इमारती, रस्ते यांचे आराखडे बनविण्यात त्रिकोणमितीची महत्त्वपूर्ण मदत होते... ग्रह आणि तारे यांची स्थाने निश्चित करणे, त्यांच्या भ्रमण मार्गाचे गणित करणे इ. त्रिकोणमिती उपयोगी पडते... त्रिकोणमितीत साइन, कॉसची मूल्य ठराविक अंतरांनंतर पुन्हा पुन्हा तीच येतात. त्यामुळे त्यांचा उपयोग आवर्ती घटनांच्या गुणधर्मांचा अभ्यास करता येतो... उदा., समुद्राच्या भरती-ओहोटी किंवा प्रकाश, ध्वनी, विद्युत्‌ प्रवाहाच्या लहरी... हे सर्व तुम्ही पुढे शिकणार आहेत. गम्मत म्हणून एक उदाहरण बघू... समुद्राकाठी हरिहरेश्वरला भरतीर्च्यावेळी जेट्टीला पाण्याचं खोली 18m, तर ओहोटीला 2m मोजली गेली. पहिली नोंद केलेली पूर्ण भरती 31.3.2021 तारखेला मध्यरात्री 12.00 ला होती. पूर्ण ओहोटी 1.4.21 सकाळी 6 वा. झाली असेल, तर या माहितीवरून जेट्टीसाठी पाण्याची खोली सांगणारे वेळा पत्रक तयार करा. याचे समीकरण K = 8cos(30 × T) + 10 असे येईल. इथे T = 0 (म्हणजे सुरवातीची रात्री 12ची वेळ), T = 1 म्हणजे एक तासांनी (रात्री 1 वाजताची) पाण्याची खोली, T = 2 म्हणजे 2 तासांनी (रात्री 2) असलेली खोली. भरती ओहोटीचं अंतर 6 तास आहे असे दिसते. समीकरण वापरून पहिल्याच दिवशी:

• *** रा. 12 वा. म्हणजे 0 तासांनी K = 8cos(30 × 0) + 10 = 8cos(0) + 10 = 8(1) + 10 = 18m
• *** स. 6 वा. म्हणजे 6 तासांनी K = 8cos(30 × 6) + 10 = 8cos(180) + 10 = 8(–1) + 10 = 2m

हे प्रत्यक्षाशी जुळते, समीकरण सिद्ध होते. इतर वेळा आणि पाण्याची खोली:

• *** स. 7 वा. म्हणजे 7 तासांनी K = 8cos(30 × 7) + 10 = 8cos(210) + 10 = 8(-0.87) + 10 = 3.04m
• *** स. 7.30 वा. म्हणजे 7.5 तासांनी K = 8cos(30 × 7.5) + 10 = 4.32m
• *** दु. 12 वा. म्हणजे 12 तासांनी K = 8cos(30 × 12) + 10 = 18m
• *** दु. 4.30 वा. म्हणजे 16.5 तासांनी K = 8cos(30 × 16.5) + 10 = 4.32m

अशा प्रकारे वेळा पत्रक काढता येईल. हे महत्त्वाचे आहे कारण मोठ्या बोटीं परत येतात तेव्हा तरंगत रहायला किमान 4m पाण्याची खोली आवश्यक असते. म्हणजे सकाळी 7.30 ते दुपारी 4.30 या वेळातच बोटी किनार्याला जेट्टीवर येऊ शकतात. हे समीकरण सोपं दिसावं म्हणून भरती ओहोटीच्या वेळ 6 तास घेतलेला आहे. प्रत्यक्षात वेळ 6 तास 12.5 मिनिट असतो. समीकरणात 30 च्या जागी 29.03 घ्यावे लागेल. मग अजून अचूक उत्तर येईल, आणि रोजच्या बदलणाऱ्या वेळा जास्त अचूक सांगता येतील... हेच तत्व उपग्रहाच्या भ्रमण कक्षाला सुद्धा लावता येईल. तुमच्या फोनवर असलेलं GPS सुद्धा ट्राएंग्युलेशन तत्वावर चालतो... सरांनी सांगितलेले उदाहरणं फारसे चांगले कळले नसले तरी त्रिकोणमिती आणि एकंदरीतच त्रिकोणाच्या गणिताचे कुतुहल वाढले होते. अगम्य वाटणारे समीकरण एव्हडे सहज नित्य उपयोगी असेल हे मात्र स्पष्ट कळले होते. संध्याकाळी पाणीपुरी आणि भेळेवर ताव मारताना, भांडण कधी मागे पडले कळलेच नाही. नेहा"काकू" पण चेष्टा स्पोर्टींगली घेत होत्या... एरेटॉसथिनिस काका काय सांगतात याची उत्सुकता वाढतच होती... ******** शनिवार: आई एस आर आर्यभट्ट वर **** एरेटॉसथिनिस काका सांगू लागले... इसवी सन ख्रिस्तपूर्व, 276 BCE मधे एरेटॉसथिनिस ऑफ सायरिन (Eratosthenes of Cyrene) यांचा जन्म झाला. ते एक अतिशय हुशार खगोलतज्ञ, गणितज्ञ, लेखक आणि कवी असे चतुरस्त्र व्यक्तिमत्व होते. ते अलेक्सझांड्रिया येथे प्रसिद्ध संग्रहालय-ग्रंथालयाचा संचालक होता. (सायरिंन – प्राचीन ग्रीक वसाहत – आता लिबिया देश, इजिप्तच्या जवळ.) एरेटॉसथिनिस जन्म झाला तेव्हा पृथ्वी गोल आहे हे सर्वमान्य झालं होतं. ती थोडी 'आसा' (axis) वर लंबकासारखी हलते हे पण सिद्ध झालं होतं. पण प्रश्न भरपूर होते आणि त्यातलाच एक मोठा प्रश्न होता मोजमाप! पृथ्वी किती मोठी आहे, त्याचा परीघ किती? हे मोजायला पृथ्वी भोवती चालावे लागणार होते, वाटेतले महासागर ओलांडावे लागणार होते. हे सर्व कसे करणार? भौगोलिक संशोधनासाठी एरेटॉसथिनिस अनेक प्रवाश्यांशी बोलत होता. मिळाललेल्या माहितीवरून पृथ्वी कशी आहे या प्रश्नांचे उत्तर शोधत होता. एके दिवशी त्याला एक वेगळीच गोष्ट ऐकायला मिळाली. जून महिन्याच्या २१ तारखेला मध्यान्ह होताच साईनी शहरात एका विहिरीत सूर्याचे प्रतिबिंब या एकाच दिवशी दिसते. विहिरीचे तोंड लहान होते आणि ती खोल पण होती. त्या दिवशी, त्या वेळेला सावली सुद्धा अदृश्य होते! (साईनी शहर – आजचे आस्वानं, नाईल नदीच्या काठावर, दक्षिण इजिप्त) अलेक्सझांड्रियाला असे काही घडत नाही. वर्षभर स्पष्ट सावली दिसते. लांबी कमी जास्त होते, पण सावली नाहीच असे कधी होत नाही. खोल आणि अरुंद विहिरीत सूर्याचे प्रतिबिंब कधीच दिसत नाही. एरेटॉसथिनिसने साईनी शहराला जाऊन सावली अदृश्य होताना प्रत्यक्ष बघितली. त्याचा लक्षात आले की सावली अदृश्य होत नाही, पायाखाली जाते. करण सूर्य बरोबर माथ्यावर येतो! त्याचा पुढच्या वर्षी त्याच तारखला त्याने अलेक्सझांड्रियाला सावलीची लांबी मोजली. इजिप्तच्या राजा टॉलेमीच्या मदतीने अलेक्सझांड्रिया ते साईनी शहर हे अंतर पुन्हा अचूक मोजले आणि मग एक गणित मांडले, ज्याने त्याला पृथ्वीचा परीघ सांगता आले. एरेटॉसथिनिसचे लिखाण काळाच्या ओघात हरवले, पण त्यांनी केलेल्या गणिताचा उल्लेख आणि स्पष्टीकरण क्लिओमीडिस नावाच्या लेखकाच्या ग्रंथात सापडतो. पृथ्वीवर पोहोचणार सूर्याचे सर्व किरण समांतर आहेत असे एरेटॉसथिनिसने गृहीत धरले, कारण सूर्य खूपच लांब अंतरावर आहे. त्यामुळे साईनी शहरात, पृथ्वीच्या पृष्ठभागावर, त्या विशिष्ट दिवशी सूर्यकिरण पूर्णपणे उभे पडतात त्यामुळे सावली पायाखाली जाते. पण पृथ्वी गोल आहे, त्यामुळे त्याच वेळेला अलेक्सझांड्रियाला पृष्ठभागावर किरण तिरके पडतात, आणि म्हणून सावली दिसते. सावलीच्या लांबीवरून, सूर्यकिरणांनी उभ्या काठीशी केलेला कोन काढता येतो, tan(x) = opp. Side (सावलीची लांबी) भागीले adj. side (काठीची लांबी). Arctan(x) = ? ... त्याचे उत्तर 7.2 अंश असे आले. 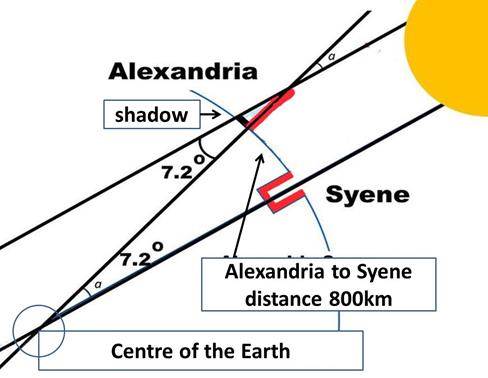एरेटॉसथिनिसचे पृथ्वीचे एक गोल चित्र काढले. गोलावर सरळ उभी धरलेल्या काठी काढली, काठी मधून जाणारी एक रेष काढली, जी गोलाच्या मध्यबिंदू मधून जाते. तसेच साईनी शहरातल्या विहिरीची खड्डा काढला आणि त्यातूनही जाणारी रेष गोलाच्या मध्यबिंदूतून पुढे नेली. साईनी शहर आणि काठीच्या मधले अंतर मांडले – 800 km (त्या काळचे ग्रीक मोजमाप 'स्टेडिया' होत). सूर्यकिरण दाखवण्यासाठी समांतर रेषा काढल्या, एक काठीच्या वरच्या टोकाला चिकटून जात होती. तिने गोलावर सावली पण स्पष्ट झाली. दुसरी सुर्यकिरणाची रेष विहिरीतली रेषवरूनच जात होती. किरणांच्या रेषा समांतर आहेत, काठीची रेष त्यांना छेदून जाते म्हणून दोन्ही आतले कोन सारखचे –7.2 अंश आहेत. क्लिओमीडिस या प्राचीन लेखकाने हे गणित समजावले आहे. गोलाच्या मध्यबिंदूचा कोन 7.2 अंश हा गोलाच्या 360/7.2 एव्हडा भाग (प्रमाण) आहे. आणि अलेक्सझांड्रिया ते साईनी शहरा पर्यंतचे अंतर हे गोलाच्या परीघाचा, परीघ/800 इतका भाग (प्रमाण) आहे. दोन्ही प्रमाण सारखे असले पाहिजे, त्यामुळे, 360/7.2 = परीघ/800, म्हणून परीघ = 360 ×800/7.2 = 40,000 km आधुनिक मोजमाप सांगते की परीघ प्रत्यक्ष 40,075 km आहे. घरात बसून केवळ गणित करून त्याने ते जवळपास अचूक सांगीतले! ************************** तुम्ही तुमच्या गावात – हा प्रयोग करून बघू शकता. खाली दिलेली वेबसाईट तुम्हाला चांगली माहिती देईल. दुसरी लिंक वापरून तुमच्या सोयीच्या दिवशी zero shadow day कुठे आणि किती वाजता आहे हे तुम्ही शोधू शकाल. मग त्या दिवशी आणि त्याच वेळी, तुमच्या घरी / गावात काठी उभी धरून सावलीची लांबी मोजा. काठीची लांबी तुम्ही सहज मोजू शकता. (तुमची स्वतःची सावली मोजली तर चालेल :-) ) आता एरेटॉसथिनिसनी जसा कोन शोधला तसा कोन शोधा. Zero shadow day असलेल्या गावाचे तुमच्या गावापासूनचे, सरळ रेषेत, अंतर किती हे गुगल करा किंवा नकाशावर मोजा. एरेटॉसथिनिसला जेव्हडी माहिती मिळाली तेव्हडी तुम्हाला मिळेल. गणित करून बघा. लिंक्स:

1. *** Astronomical Society of India - The Public Outreach & Education Committee
2. *** कुठ्ल्याही गावासाठी सावली गायब होणारे २ दिवस आणि वेळ हा अँप वापरून बघा

************************** एरेटॉसथिनिस काका सांगत होते ... आता आपल्याला समद्विभुज खंडावर जायचे आहे. खंड तर पाहूच, पण प्रशासनानी काही काम दिले आहे. या निमित्ताने तिथे जायला मिळाले आहे. मुख्य शहर तर देखणे आहेच, पण तिन्ही किनार्यावर बीच बघण्यासारखे आहेत. प्रशासनाला संपूर्ण बेटा भोवती फिरणारी रिंग रेल्वे असा प्रकल्प करायचा आहे. बेटाची एक बाजू 1200 km, तर दुसऱ्या दोन बाजू 1000 km आहेत. तिन्ही किनार्याला स्पर्श करून रेल्वे धावली पाहिजे. भूगोल पाहता रस्ता गोलाकार वाटतोय/हवा आहे. उंच सखल भागही फारसे नाहीत, त्यामुळे रूळ टाकणे 1 लाख रुपये प्रति km हा दर ठीक वाटतो. 40 लाख प्रत्येक बाजूला 3 मुख्य स्टेशनसाठी आणि 20 लाख मधल्या 3 स्टेशनसाठी. 10 टक्के अवांतर खर्च जोडायला हरकत नाही. अंदाजपत्रक (एस्टीमेट) द्यायचे आहे. मला अजूनही बरेच काम दिले आहे, तेव्हा प्लीज तुम्ही माझ्यासाठी हे काम करा. ************ क्रमशः ***** वाचकहो - तुम्ही सुद्धा प्रयत्न करा. हे पण करून बघा:

1. काठीची उंची २ मीटर होती, तर सावलीची लांबी किती?
2. तसेच, पृथ्वीचा radius किती?

************************** गोष्टीचा पुढचा भाग... लवकरच **************************