पूर्वपीठिका
सध्या मी राहतो तिथे उन्हाळा चालू आहे. दक्षिण गोलार्धात असल्यामुळे इथले ऋतू आपल्यापेक्षा उलटे चालतात. त्यामुळे सध्या जिकडे तिकडे भसाभस मुंग्या अन्नाच्या शोधार्थ बाहेर पडत आहेत. लहान असताना उन्हाळ्याच्या सुट्टीत ह्या मुंग्यांची मजा बघत बसणे हा एक आवडता छंद झाला होता. घरात कुठे मुंग्या लागल्या असतील तर त्यांची रांग बघत बघत मूळ स्रोत शोधायचा प्रयत्न करणं, रांगेच्या मध्येच बोटाने पुसून त्यांची रांग अस्ताव्यस्त करणं, मुंग्यांच्या भोवती पाणी शिंपडून त्याचं वर्तुळ करणं आणि मुंग्यांना हा भवसागर पार करून जाता येतं का ते पाहणं - असले अनेक उद्योग तेव्हा केलेत! अन्नाची तजवीज म्हणून मुंग्या डोक्यावर साखरेचे कण घेऊन जाताना पाहिलं आहे. त्यांना एकमेकीशी भांडताना सुद्धा पाहिलं आहे. पण कधीतरी प्रश्न पडायचा की ह्या एकमेकींना साखर फेकून का मारत नाहीत?
तसा तेव्हा फार काही सखोल विचार केला नव्हता! तसं कधी वाघ - सिंह वगैरे मंडळी पण एकमेकांना काही फेकून मारत असल्याचं ऐकलं नाहीये. पण मुळात त्यांना हाताने (किंवा पायाने) काही जड वस्तू अशी उचलतानाच पाहिलेलं नाहिये, त्यामुळे फेकायचा प्रश्नच नाहिये. मुंग्या मात्र त्यांच्या स्वतःच्या वजनापेक्षा जास्त वजनाचा साखरेचा कण लीलया उचलतात, त्यामुळे त्यांच्याकडे हे पोटेन्शियल असलं पाहिजे, असं कधीतरी डोक्यात चमकून गेलं असेल. नंतर इंजीनियरिंग करत असताना हा विचार पुन्हा चालू झाला आणि थोडंफार वाचन केल्यावर काही उत्तरं सापडत गेली. त्या उत्तराचा प्रवास मी इथे ३ भागांमध्ये देत आहे. पैकी पहिला भाग हा लहान आणि मोठे जीव ह्यात काही आकारामुळे फरक असतो का, ह्या मूळ प्रश्नाशी निगडित आहे. त्यातल्या काही गमती जमतींमधून कळलेल्या आणखी काही गोष्टी भाग २ मध्ये आणि ह्या दोन्हींमधून कळलेल्या विज्ञानाचा परिपाक म्हणून कळालेलं उत्तर शेवटच्या भागात आहे.
तर भाग २ चे नाव आहे, 'काय म्हणाले हॅल्डेन काका?'
हा लेख २०१५-१६ मध्ये महाराष्ट्रातील काही शाळांमध्ये एका वाचन-प्रकल्पाचा भाग म्हणून वापरण्यात आला आहे. त्यात आवश्यक बदल करून येथे देत आहे. या भागापूर्वी पार्श्वभूमीकरिता कृपया भाग १/३ वाचणे.
मागच्या भागात आपण पाहिलं की एखाद्या प्राण्याचा आकार जसाच्या तसा वाढवत नेला, तर त्याचं घनफळ जितक्या प्रमाणात वाढेल, त्याच्यापेक्षा कमी प्रमाणात त्याचं क्षेत्रफळ वाढतं. इथे हे गृहीत धरलं आहे की त्या प्राण्याची उंची जर दुपटीने वाढली तर रुंदी देखील दुपटीनेच वाढेल. या न्यायाने लहान असताना तो प्राणी जसा दिसतो, तसाच्या तसा तो मोठा झाल्यावर दिसेल. म्हणजे त्या पौराणिक मालिकांमध्ये माणसे लहान-मोठी होतात त्याप्रमाणे. पण प्रत्यक्षात प्राणी असे वाढतात का? आपलंच उदाहरण घ्या. एखादं लहान बाळ मोठं झाल्यावर जर तश्याच शरीराच्या रुंदी-उंची प्रमाणात राहिलं असतं तर त्याची सावली खालील चित्राप्रमाणे दिसलं असतं (चित्रात पहिली आणि दुसरी सावली पहा). पण मोठा झालेला माणूस चित्रातल्या उजव्या बाजूच्या आकृतीप्रमाणे दिसतो. किंबहुना ती मोठ्या माणसाची सावली असेल हे तुम्हाला आपोआप जाणवलं असेल.
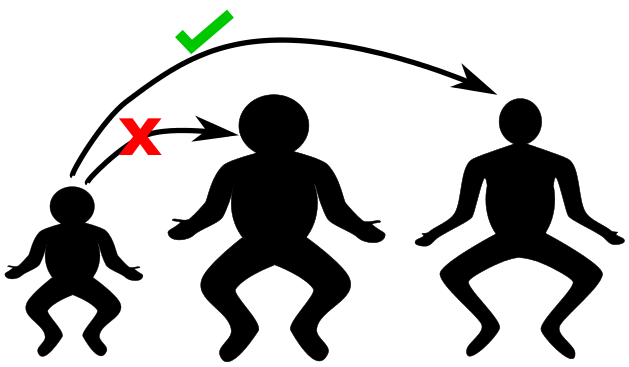
चित्र १: लहान बाळाची सावली वा मोठ्या माणसाची सावली पहा. बाळ जसंच्या तसं मोठं न होता हातापायांची लांबी लांबी वाढते.
वरच्या चित्रात दोघांना जर नीट पाहिलं तर लक्षात येईल की पूर्ण वाढ झालेल्या त्या माणसाचं डोकं साधारणपणे त्या लहान बाळाच्या इतकंच असेल परंतु हात-पाय फारच लांब आहेत. म्हणजे माणसाच्या शरीराची वाढ सर्व बाजूंनी सारखी न होता उंचीच्या दिशेने जास्त होते. आपल्या डोक्याच्या आकारात लहानपणापासून अगदी खूप काही फरक पडत नाही (बघा! आपल्याला वाटतं आपण फार शिकलो!). आपला घेर देखील साधारण दीड ते दोन पटीने वाढतो (तुम्ही अपवादात्मक स्थिती मध्ये आहात का?), पण उंची मात्र ५-६ पट वाढते. म्हणजे, एखादी दंड-आकृती (cylinder) फक्त उंचीच्या बाजूने वाढवत न्यावी तशी आपली वाढ होते. आपलं शरीर ही एक दंड-आकृती समजली तर त्याचं घनफळ (pi*r*r*h) एवढं होईल, जिथे r म्हणजे आपली त्रिज्या आणि h म्हणजे उंची होय. आपली त्रिज्या (r) फार न बदलता फक्त उंची (h) वाढवली तर घनफळ हे h च्या पटीत वाढेल. शिवाय क्षेत्रफळ देखील अन्दाजे h च्या पटीत वाढेल. त्यामुळे मागच्या भागात सांगितलेल्या घनाप्रमाणे आपली वाढ न होता दंडाप्रमाणे होईल. अश्या परिस्थितीत आपल्याला ऊर्जा-संक्रमणाचा प्रश्न तितकासा सतावणार नाही.
आता लहान आणि मोठ्या प्राण्यांच्या शरीरात असा कोणता फरक असतो की ज्यामुळे त्यांनाही त्यांचा आकार आणि शरीराचे ऊर्जा संक्रमण हे प्रश्न सतावत नाहीत? एक लक्षात घ्या, की आपल्या शरीरात मांसल भाग/उती (tissues) जेवढे असतील त्या प्रमाणात उष्णता निर्माण होते. जर प्राणी त्यांच्या लहानपणी आणि मोठेपणी सारखेच दिसू लागले (म्हणजे वरच्या चित्रातल्या लहान आणि मोठ्या बाळासारखे), तर त्यांच्या शरीरात एकूण आकारमानापैकी मांसाची असणारी टक्केवारी सारखीच राहील. त्यामुळे आकारमान (किंवा घनफळ) जितक्या प्रमाणात वाढलं आहे तितक्या प्रमाणात शरीराची उष्णता वाढेल, पण ती उष्णता बाहेर टाकण्यासाठी शरीराचा पृष्ठभाग तेवढा नसेल. ह्याचं कारण आपण मागच्या भागात पाहिल्याप्रमाणे जर एखाद्या गोष्टींची लांबी-रुंदी-उंची सम-प्रमाणात (‘क्ष’ पटीने) वाढवली, तर त्याचं घनफळ त्या पटीचा तिसऱ्या घाताएवढं (क्ष*क्ष*क्ष) आणि पृष्ठभागाचे क्षेत्रफळ दुसऱ्या घाताएवढं (क्ष*क्ष) वाढेल. हा नियम पाहता असा प्रश्न पडेल, की मग हत्तीसारख्या मोठ्या प्राण्यांमध्ये कितीतरी जास्त प्रमाणात उष्णता निर्माण होत असणार! त्यांची पंचाईत नाही का होणार?
प्रत्यक्षात मोठ्या आणि लहान प्राण्यांमध्ये हा एक मूलभूत फरक आहे. त्यांच्या शरीरात मांसाची टक्केवारी वेगवेगळी असते. उरलेला भाग हा जास्त मोठ्या हाडांनी व्यापला जातो. म्हणजे मोठ्या प्राण्यांमध्ये उष्णता बाहेर फेकायला पृष्ठभाग कमी असल्यामुळे ते मुळातच उष्णता कमी निर्माण करतात, ज्यासाठी त्यांच्या अंगात मांस अपेक्षेपेक्षा कमी असतं, आणि हाडं जास्त प्रमाणात असतात. लक्षात घ्या, मोठ्या प्राण्यांमध्ये मांस लहान प्राण्यांपेक्षा नक्कीच जास्त आहे, पण त्यांच्या एकूण शरीराच्या मानाने टक्केवारी काढली तर ती कमी भरेल. आता खाली दिलेल्या आकृतीमध्ये वेगवेगळ्या प्राण्यांचे सापळे दिले आहेत. तुम्हाला कदाचित त्यातले काही प्राणी केवळ आकारावरून ओळखता येतील. सगळ्यात सोपा ओळखण्याजोगा प्राणी म्हणजे हत्ती, तो त्याच्या सोंडेमुळे. आता माणूस आणि गोरिला सापडत आहेत का पहा. त्यात माणसाच्या हाडांची जाडी पहा आणि गोरिलाच्या हाडांची पहा. कुणाला जास्त वजन पेलावे लागते? (प्राणी ओळखायला अवघड जात असल्यास मूळ चित्राचा हा दुवा पहा. त्यात ज्या सापळ्यावर क्लिक कराल, त्या प्राण्याची माहिती दिसेल.)

चित्र २: विविध प्राण्यांचे सापळे.
मोठ्या प्राण्यांना त्याचं वजन पेलण्यासाठी हाडांचं आंतरछेदीय क्षेत्रफळ (cross-sectional area) जास्त असणं महत्वाचं असतं. त्यामुळे लहान प्राणी जसेच्या तसे मोठे केले आणि त्यांचं हाडांचं प्रमाण सारखंच ठेवलं तर हाडांचं घनफळ वाढेल पण त्यांचं आंतरछेदीय क्षेत्रफळ त्या प्रमाणात वाढलं नसेल. त्यामुळे हत्तीसारख्या प्राण्यांना वजन पेलण्यासाठीही जास्त मोठ्या हाडांची गरज असतेच. त्याचप्रमाणे गोरलाची हाडंदेखिल माणसांच्या हाडांपेक्षा जास्त जाड दिसतात, कारण जास्त वजन पेलण्यासाठी ते आवश्यकच आहे. कदाचित निसर्गाने प्राणी उत्क्रांत होताना उष्णता, वजन आणि अश्या अनेक घटकांची काळजी घेतली असावी आणि म्हणून लहान-मोठे प्राणी हे असे वेगवेगळ्या आकाराचे, तोंडांचे, पोटाचे, पायांचे तयार झाले असावेत. कुणाचे पाय उंच, कुणाची मान उंच, कुणाचं शरीर लहान आणि पाय मोठे - हे सगळे एकाच वेळी एकाच ग्रहावर एकाच वातावरणात तग धरून राहतात! कदाचित निसर्गाने वेगवेगळी कॉम्बिनेशन्स करून पहिली असतील आणि तग न धरू शकणारे उष्णतेने, हात-पाय मोडून आणि इतर अनेक प्रकारे नष्टही झाले असतील. शिवाय अन्न मिळविण्यासाठीची पद्धत, शिकारीची पद्धत, स्वतःचा इतर प्राणी आणि नैसर्गिक आपत्तींपासून बचाव करण्याची पद्धत - असे अनेक विषय हे वैशिष्ट्यपूर्ण शरीररचना उत्क्रांत होताना कारणीभूत ठरले असतील. तूर्तास फक्त शरीराचे आकारमान ह्यावर लक्ष देऊ. विशेष म्हणजे हा, वरवर अतिशय सोपा वाटणारा, वर्ग-घन नियम (square-cube law) वापरून निसर्गातील अनेक गोष्टींचा उलगडा होतो, हे दखल घेणासारखं आहे!
२० व्या शतकात जे.बी.एस. हॅल्डेन नावाचा एक इंग्रज शास्त्रज्ञ होऊन गेला. अतिशय भन्नाट माणूस! १९२८ च्या सुमाराला त्याने 'on being the right size' नावाचा एक निबंध प्रकाशित केला, ज्याने जीवशास्त्रावरच्या संशोधनात खळबळ उडवून दिली. अमुक एक प्राणी हा अमूक एक आकाराचाच का आहे, अश्या गोष्टींची उत्तरं त्याने शोधायचा प्रयत्न केला आणि त्याला असं लक्षात आलं की शाळेत शिकलेला सोपा 'वर्ग आणि घनाचा नियम (स्क्वेअर-क्यूब लॉ)' वापरून बऱ्याच प्रश्नांची उत्तरं मिळतात. आपण हा नियम वापरून वरती उष्णता आणि वजन ह्या गोष्टी पहिल्या. पण केवळ ह्याच नाही, तर ‘प्राण्यांमध्ये असणारी प्राणवायू घेण्याची यंत्रणा, प्राण्यांची ताकद, त्यांची बचाव करण्याची पद्धत’ अश्या अनेक विषयांना त्याने हा 'वर्ग आणि घनाचा नियम’ वापरून त्या गोष्टी समजावून सांगितल्या.

चित्र ३: जे.बी.एस. हॅल्डेन.
हॅल्डेनचं आयुष्य देखील अफलातून आहे. हॅल्डेनचा जन्म आणि शिक्षण इंग्लंडमध्ये झालं. ऑक्सफर्डसारख्या ठिकाणी शिकून हा पहिल्या महायुद्धात ब्रिटीश आर्मीकडून लढला. युद्धानंतर पुन्हा ऑक्सफर्डमध्ये संशोधनास लागला. नंतर केम्ब्रिज विद्यापीठात जीव-रसायन शास्त्र शिकवू लागला. वयाच्या ४० व्या वर्षी तो जनुकीय विज्ञान (genetics) विषयातील प्रोफेसर बनला. आणि त्यानंतर साधारण १३ वर्षांनी तो भारतात आला. त्यानंतर त्याने उर्वरित आयुष्य भारतातच घालवलं. तो एक उत्तम गणितज्ञही होता. कलकत्त्याला भारतीय सांख्यिकीय संस्थान (Indian Statistical Institute) मध्ये काम करून भारताच्या सांख्यिकी (statistics) आणि जीवमिती (biometry) विषयांच्या शिक्षणात महत्त्वाचं योगदान दिलं. त्याला इंग्लंड सोडून भारतात जाण्याचं कारण विचारलं असता त्याने 'मला आता यापुढे पायात मोजे घालावे लागणार नाहीत' असं मजेशीर कारण सांगितलं होतं! मार्क्सवादी असणारा हा शास्त्रज्ञ स्वभावाने अतिशय विनोदी होता. मृत्युपूर्वी कर्करोगाने आजारी असताना देखील भुवनेश्वरमध्ये हॉस्पिटलमध्ये बसल्या बसल्या त्या रोगावरही त्याने विनोदी कविता लिहिली.
असो. प्राण्यांच्या आकारानुसार ते काय काय प्रकारचं बल लावू शकतील हे सुद्धा बदलतं. आता मुंग्यांच्या बाबतीत ते कसं कामाला येईल? मुंग्यांच्या हालचालींना कुठल्या गोष्टींमुळे अवरोध निर्माण होऊ शकतो? फेकून मारण्यासाठी कशा प्रकारचं बल लावायला लागेल? पाहूया पुढच्या भागात.
- शंतनु
संदर्भ:
१. On being the right size, by J. B. S. Haldane, from Possible Worlds and Other Essays (1926)
२. चित्र क्र. २ आणि ३ विकिपीडियाच्या सौजन्याने


प्रतिक्रिया
21 Jan 2019 - 5:03 pm | प्रमोद देर्देकर
खूप छान अगदी बाळबोध होवून शिकवण चालू आहे .
धन्यवाद
कृपया थोडे मोठे भाग लिहीत चला.
22 Jan 2019 - 9:49 am | पुष्कर
हा भाग छोटा झाला आहे खरा! मान्य आहे.
आपला,
बाळबोध पुष्कर :) :)
22 Jan 2019 - 10:30 am | ज्ञानोबाचे पैजार
दुसरा भागही आवडला.
शाळेत गणिताचे शिक्षक कधी शास्त्रा बद्दल बोलले नाहीत ना शास्त्राचे शिक्षक शास्त्र सोडून दुसर्या कोणत्या विषया बद्दल.
पण इथे भुमिती, भौतिकशास्त्र आणि जीवशास्त्र यांची सांगड घातलेली पाहुन एकदम अरे?? असे झाले. खरं तर असाही विचार करता येतो अशी जाणिव (मला तरी) या आधि फारशी तिव्रतेने झाली नव्हती.
शाळेतले शिक्षण शाळेतच राहिले आणि कॉलेज मधले कॉलेजातच.
पैजारबुवा,
22 Jan 2019 - 11:42 am | अनिंद्य
ज्ञानकण वेचतोय, लेख वाचनीय !